Home
News
How ?
Download
Bench
Status
Reserve
Submit
Results
Producers
Math.
Algo.
Stat.
Fun

Links
Credits
Feedback		  

How many prime numbers appear in a sequence ?

Based on Bateman and Horn conjecture [1], which is the quantitative form of the famous "Hypothesis H" of Sierpinski and Schinzel [7], and on the distribution of the factors of the generalized Fermat numbers [3], Harvey Dubner and Yves Gallot proposed in [2] the following conjecture:

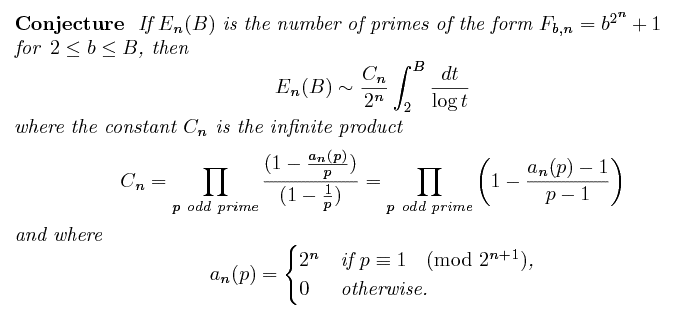
Daniel Shanks computed C1 and C2 to high precision [5] [6]. Recently, Peter Moree indicated a method for the computation of the Cn by representing them as a product of Dirichlet L-series. Yves Gallot used this method to compute precisely C1 , C2, ..., C17 [4]. These results are used for the following estimates.

Computation of the expected number of GF primes in a fixed range
and of the associated Poisson distribution
N = bMin = bMax =
Expected number
of GF primes
Poisson distribution

The estimates and actual values of the number of known GF primes are shown in the following table. We assume that the distribution of GF primes is approximated by a Poisson distribution and the error is defined by (Act. - Est.) / sqrt(Est.).

n N B Cn estimate actual error
1 2 109 1.3728134628182460091 34903256 34900212 -0.5
2 4 108 2.6789638797482848822 3859187 3857543 -0.8
3 8 107 2.0927941299213300766 173942 174368 +1.0
4 16 107 3.6714321229370805404 152575 152447 -0.3
5 32 107 3.6129244862406263646 75072 74951 -0.4
6 64 107 3.9427412953667399869 40963 41059 +0.5
7 128 9 106 3.1089645815159960954 14638 14586 -0.4
8 256 7 106 7.4348059978748568639 13848 13890 +0.4
9 512 6 106 7.4890662797425630491 6042 6138 +1.2
10 1024 5 106 8.0193434982306030483 2730 2614 -2.2
11 2048 4 106 7.2245969049003170901 1000 1000 0.0
12 4096 3 106 8.4253498784241795333 446 435 -0.5
13 8192 2.6 106 8.4678857199473387694 196 190 -0.4
14 16384 2.7 106 8.0096845351535704233 96 89 -0.7
15 32768 2.2 106 5.8026588347082479139 29 35 +1.1
16 65536 1.1 105 11.195714229391949615 1.8 2 +0.2
17 131072 3 104 11.004300588768807590 0.3 0 -

References

  1. P. T. Bateman and R. A. Horn, A Heuristic Asymptotic Formula Concerning the Distribution of Prime Numbers, Math. Comp. 16 (1962), 363-367. MR 26:6139
  2. H. Dubner and Y. Gallot, Distribution of Generalized Fermat Prime numbers, Math. Comp. 71 (2002), 825-832. http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-01-01350-3
  3. H. Dubner and W. Keller, Factors of generalized Fermat numbers, Math. Comp. 64 (1995), 397-405. MR 95c:11010
  4. Y. Gallot, A Problem on the Conjecture Concerning the Distribution of Generalized Fermat Prime numbers (a new method for the search for large primes), Preprint.
  5. D. Shanks, On the Conjecture of Hardy & Littlewood concerning the Number of Primes of the Form n2+a, Math. Comp. 14 (1960), 321-332. MR 22:10960
  6. D. Shanks, On Numbers of the Form n4+1, Math. Comp. 15 (1961), 186-189. MR 22:10941
  7. A. Schinzel and W. Sierpinski, Sur certaines hypothèses concernant les nombres premiers, Acta Arith. 4 (1958), 185-208, Erratum 5 (1959), 259. MR 21:4936